In this study, we revisit the densest binary sphere packings (DBSPs) under periodic boundary conditions and present an updated phase diagram, including newly found 12 putative DBSPs over the $x-\alpha$ plane, where $x$ is the relative concentration and $\alpha$ is the radius ratio of the small and large spheres. You can download this paper here.
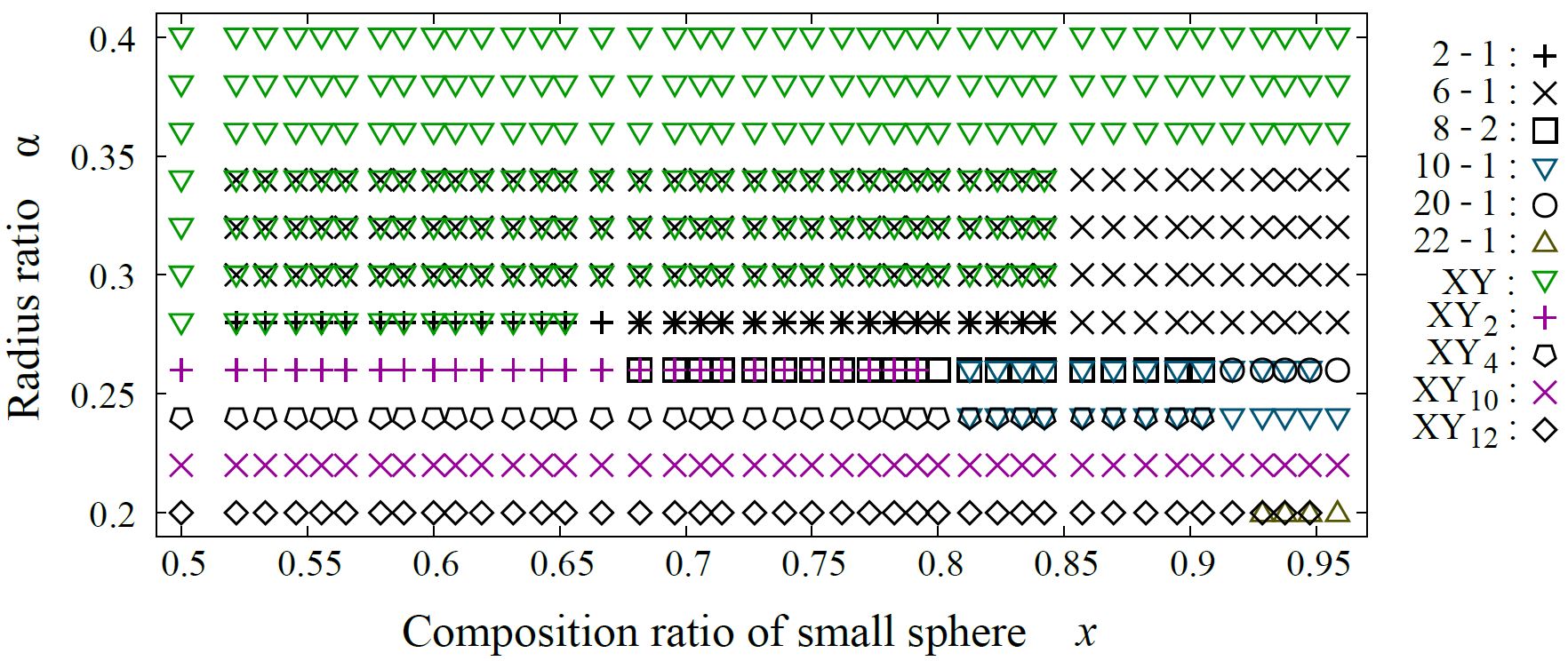
    For $0.20 \le \alpha \le 0.40$, the exhaustive search is conducted for 11 radius ratios of $0.20$, $0.22$, $0.24$, $0.26$, $0.28$, $0.30$, $0.32$, $0.34$, $0.36$, $0.38$, and $0.40$. In order to confirm that the (12-1) structure appears on the phase diagram, the XY₁₂, XY₁₁, and (22-1) structures are re-optimized at $\alpha = 0.203$. The number of spheres in the unit cell is set between 6 and 24. As a result, we have identified the new six putative DBSPs: the XY₁₂, (22-1), (12-1), (20-1), (8-2), and the (2-1) structures.
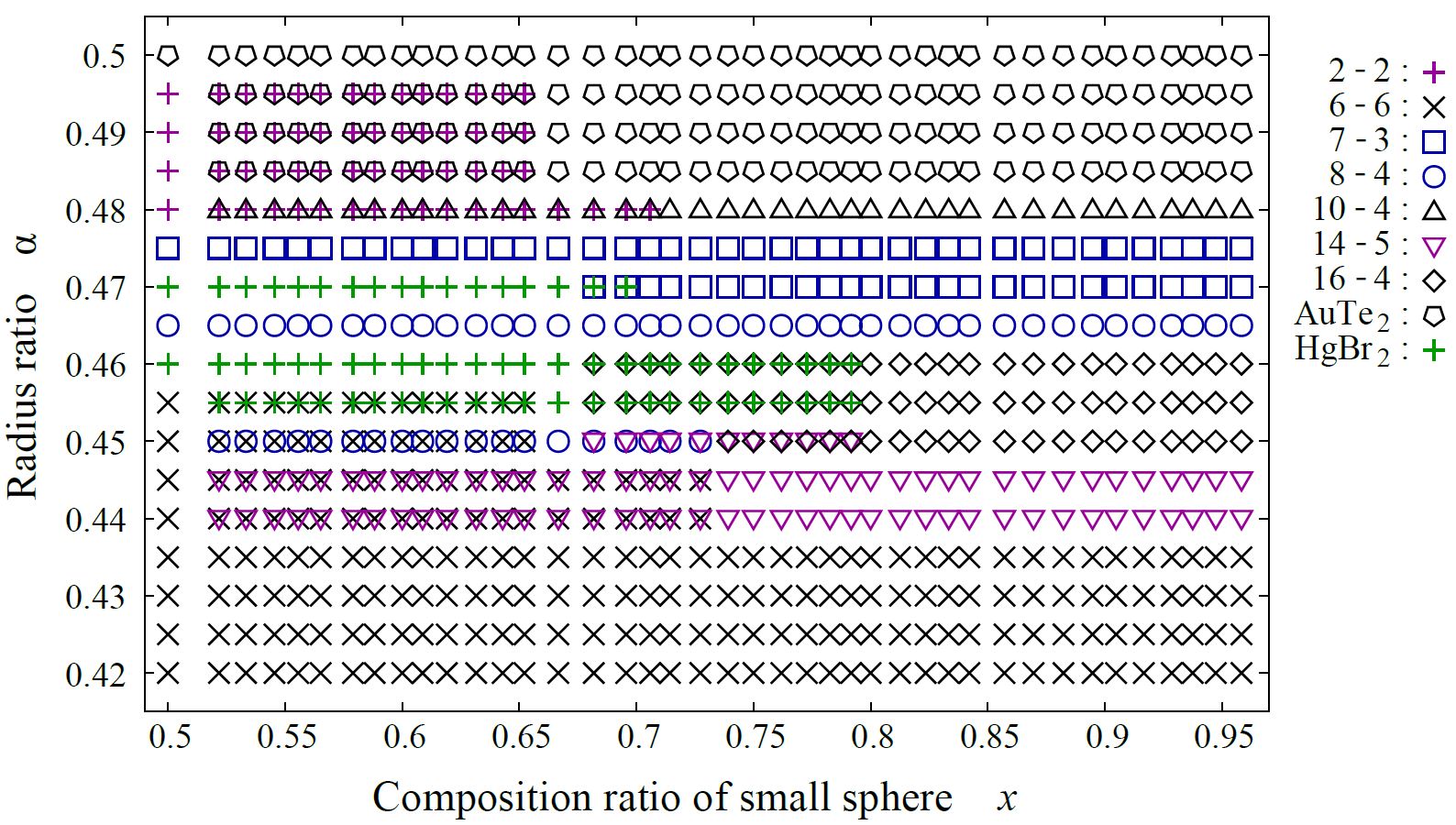
    For $0.420 \le \alpha \le 0.500$, the exhaustive search is conducted for 17 radius ratios of $0.420$, $0.425$, $0.430$, $0.435$, $0.440$, $0.445$, $0.450$, $0.455$, $0.460$, $0.465$, $0.470$, $0.475$, $0.480$, $0.485$, $0.490$, $0.495$, and $0.500$. In order to confirm that the (9-4) structure appears on the phase diagram, the (2-2), (10-4), AuTe₂, and (9-4) structures are reoptimized at $\alpha = 0.481$, $0.482$, and $0.483$. The number of spheres in the unit cell is set between 12 and 32. As a result, we have identified 5 new putative DBSPs: the (14-5), (16-4), (8-4), (10-4) , and (9-4) structures.
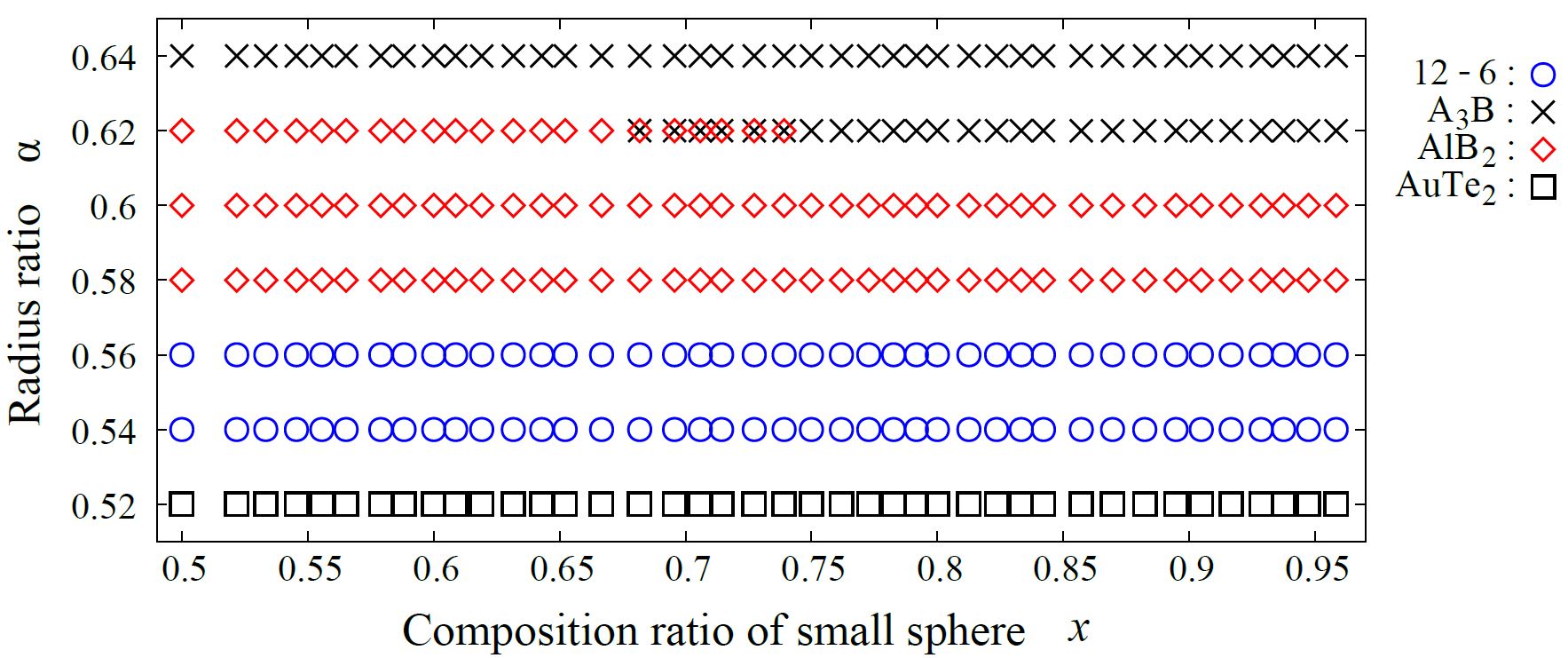
    For $0.52 \le \alpha \le 0.64$, the exhaustive search is conducted for 7 radius ratios of $0.52$, $0.54$, $0.56$, $0.58$, $0.60$, $0.62$, and $0.64$. The number of spheres in the unit cell is set between 6 and 24. As a result, we have identified one new putative densest packing: the (12-6) structure.
    The XY_n structure is defined as DBSP in which large spheres X constitute the fcc densest structure and small spheres penetrate into the tetrahedral and octahedral sites constituted by X. If the XY _n are excluded, there are 21 putative DBSP on the phase diagram. Most of those structures are named as ($m$-$n$) structure. A ($m$-$n$) structure contains $m$ small spheres and $n$ large spheres. The phase diagram is shown in this page, and you can download the three-dimensional data of the DBSPs.

    When the highest packing fraction is achieved by phase separation into densest binary packing R and the fcc densest packing constituting of small spheres, only the symbol of the densest binary packing R is plotted. On the other hands, when the highest packing fraction is achieved by phase separation into two densest binary packings, those two symbols are plotted together.
    The three-dimensional data of the DBSP for the phase diagram are downloadable here. The structure data are given by the dat files and the cif files. The dat files can be viewed by OpenMX viewer. The root directory contains 35 directories, which correspond to the 35 radius ratio. Those child directories contains a few directories which contains the structural data of DBSP. The structural data files are named by their packing fractions.